Failures of The Law of One Price

Using a simple model of price dispersion

In price theory, we often talk about THE price of apples, or THE wage rate, as if there is a single price for every good. This comes naturally out of our basic model where there is a single market-clearing rate; the unique intersection of supply and demand determines the market price.

But when we look out into the world, we see different prices for what seems like “the same good.” Instead of there being a single price for a good, there is “price dispersion.”

Why is that so? In this newsletter, first, I want to review three common explanations that economists give. In a bit of self-centered advertising, I will finish the newsletter by explaining my own price-theoretic model of price dispersion.

Jedi Mind Trick

The first response is that economists can try to perform a Jedi mind trick and say “there is no price dispersion.”

The law of one price tells us that the same goods must sell for the same price. Therefore, this logic says that if we see different prices for what we think of as “the same good”, that just means the two goods are not the same.

This makes sense. A Coke in a baseball stadium at $6 is not the same good as a Coke at a gas station for $2. Even though the physical product is the same, the value to buyers and the cost to sellers may vary across the two venues, so this is not the same good. Just as apples and oranges do not need to have the same price, neither do the two distinct Cokes.

This response has appeal. Because economists are subjectivists about value, we really can’t say definitively what “the same good” means. It is in the eye of the buyers and sellers.

The problem with this response is, if taken too seriously, it devoids the economic theory of content. By definition, it rules out the possibility of price dispersion. That’s fine sometimes, but if we want to study forces that affect what-appears-to-be-price-dispersion, we cannot take this too seriously. I think we should be wary of this response.

Disequilibrium Price Dispersion

Another approach is, as I suggested in a previous newsletter, to take supply and demand seriously but not literally. Yes, where supply and demand cross is the market-clearing price, and that will be a unique price with no price dispersion. But before equilibrium is reached, there may be trades that occur at different prices.

In the lab, like in Vernon Smith’s classic 1962 JPE, this story makes a lot of sense, and we can directly observe price dispersion. For example, Smith’s paper plots a bunch of different supply and demand schedules (left) and the traded price in different periods (right). One example is below.

Because of how the experiment is set up, all trades are of “the same good,” so we do not need to worry about the Jedi mind trick. The experimenter induces supply and demand, which means we know what the unique market-clearing price is. But we can also observe the trades along the way, which will not always be at the market-clearing price. We can directly see the price dispersion on the plot above.

From a theoretical perspective, this appeal to disequilibrium is a bit unsettling. We don’t have a great theory of disequilibrium pricing and adjustment; the theory may fall into “anything goes” territory again. Moreover, any disequilibrium theory cannot explain persistent price dispersion, at least if the story suggests some tendency toward equilibrium, as most models do. Again, I’m hesitant about this perspective on price-dispersion.

Search Costs

The most well-known theory of price dispersion goes to the great price-theorist George Stigler, both in his classic article on “The Economics of Information" and the opening of his textbook (HT: Rob Szarka for reminding me it was in the textbook.)

In Stigler’s formulation, unlike supply and demand, prices are not public. Each seller sets its own price and the buyers do not know the prices. To discover the prices, any buyer needs to physically visit the store. That is costly.

Unlike a Walrasian market, the firm that undercuts the others’ prices by a penny does not immediately get the entire market. The search frictions stop prices from being driven completely to a single price, so price dispersion may remain.

At this level of abstraction, the search theory suffers from the same problem as the Jedi mind trick. Anything goes. But, as Stigler argues, with a bit more structure, the theory does have teeth. For example, we can make the search costs more concrete by thinking of it as the “time” to find the good. If the value of time is roughly constant, then we can pin down some of the costs of search.

If time is a constant value, then you will not search for prices on cheap goods. Suppose you think you could say 10% at the next store. For a $1 candy bar, you won’t bother searching to save 10 cents, so we could expect a large dispersion (in percentage terms) to remain. However, for a car, 10% is a big deal and it is worth going to the next store. So we would expect to find prices to be closer together for big-ticket items. Stigler gives some evidence for this.

More important than Stigler’s exact model, the search-theoretic framework has generated lots of testable predictions. Some that fit some data. Others that miss other data. But Stigler’s theory has teeth.

Strategic Firm Price Dispersion

While Stigler’s theory is important, I see two potential problems. First, it only accounts for price dispersion that occurs at the market level. Different firms set different prices so only at the market level there is price dispersion. Second, Stigler’s search model, at least to this economist’s simplistic reading, seemed disconnected from standard price-theoretic models.

In my paper “Price Competition and the Use of Consumer Data,” I build a model of price dispersion that avoids these two problems. Firms move their own prices around, as in Hal Varian’s model of sales. So we have price dispersion (through time) by a particular firm.

I also show how the model can be solved using some simple observations about the relevant marginal revenue and marginal cost curves, so a dummy like me can understand it.

Before we get to the model, let’s ask: when would a firm be willing to charge different prices within the same market?

We know from our models of price-setting, such as monopoly, any firm is only going to charge a price that induces a quantity such that marginal revenue equals marginal cost (MR=MC). If a firm is willing to pick different prices, it must be that they correspond to multiple quantities where MR=MC.

At first, it may seem quite improbable that MR=MC for multiple quantities. Under our standard assumptions, MC slopes up, MR slopes down, and they cross at one point. Therefore, it seems that price dispersion would also be highly unlikely to see.

It is unlikely until we think a little deeper about what the demand curve is. In general, the demand curve that matters for price setting is a residual demand curve, that depends on other firms’ pricing behavior. The demand curve doesn't fall from the sky but is instead an equilibrium object governed by the forces of competition.

As we stress in this newsletter, all markets and prices are interconnected.

This is about to get a little weird, so you’ve been warned.

Let’s get to the model. Suppose there are two sellers (Best Buy and Target) who can produce a good at a constant marginal cost, which we can normalize to zero. Suppose there are a bunch of buyers, but there are three types. One-quarter of the buyers only want Best Buy’s good and are willing to pay $100 and one-quarter of the buyers only want Target’s good and are willing to pay $100. We can call these buyers “loyal.” Half of the customers are willing to pay $100 but are not loyal and will buy from the cheapest seller.

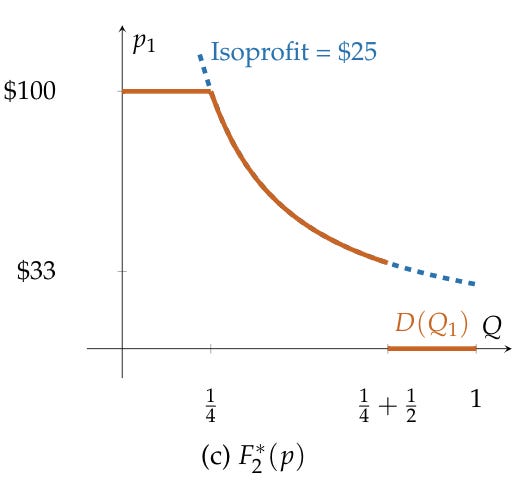
First, suppose Target is setting price equal to marginal cost, which is zero. We can plot Best Buy’s residual demand curve. If Best Buy charges a price of $100, it can sell to its loyal customers (1/4th of the population). We can find Best Buy’s best-response by looking for the highest isoprofit curve, subject to the residual demand curve. If Target set’s a price of zero, Best Buy maximizes profits by setting price equal to $100 and getting only its loyal buyers. That price generates an expected profit of $25 per person.

But this is not an equilibrium, since Target’s price of zero is not optimal.

We can first now, how high could Target raise its price, without changing Best Buy’s behavior? The answer is $33.333333. Let’s call it $33.

To see this, again plot Best Buy’s residual demand, when Target sets a price of $33.

If Target raised its price to $33, Best Buy would be indifferent between charging a price of $100, getting 1/4 of the customers, which gives a profit of $25, and charging a price of $33 and getting all of the customers that are not loyal to Target (3/4th of the population), which is a profit of $33 x 3/4, which is roughly a profit of $25.

Both prices, $100 and $33, are both the highest isoprofit points for Best Buy, given Target’s pricing.

Now here is where price dispersion explicitly comes in. Suppose that instead of a single price, Target can randomize its price. It can use price dispersion; we can think of these as sales. Importantly, Target Best Buy does know the exact price that Target picks today, so Best Buy has to best-respond to the price distribution of Target.

Target can randomly raise its prices above $33. The best Target can do is to raise its prices in such a way as to keep Best Buy on the same isoprofit curve for every price between $100 and $33.

Best Buy and Target are identical, so Best Buy’s optimal pricing also involves a distribution over all prices between $33 and $100. You can check out the paper to verify that this is an equilibrium.

Now let’s tie this back to MR=MC.

Marginal cost is zero everywhere. Given this equilibrium residual demand curve, the marginal revenue is zero for all quantities between 1/4 and 3/4. You can see this because profit=revenue and profits are equalized on the isoprofit curve. Marginal profits are zero, so are marginal revenues.

Now we have a theory of why MR=MC at many locations. It’s not just simple chance. Target, by doing the best it can, by competition for profits, will induce a residual demand curve for Best Buy that has MR=MC over some interval.

Equilibrium competition drives the MR=MC condition. It’s not simply picked by a firm.

Now my model isn’t perfect. Referees have made that clear. For example, it involves a complicated randomization strategy by the firms. But I like it (even if referees don’t) because it generates equilibrium price dispersion, using standard tools: demand curves, marginal revenue curves, etc.